 |
PMTٹضگ”‚ئ‚حپH
|
PMTٹضگ”‚حپAپ›‰~‚ًپ›پ“‚ج—ک—¦‚إژط‚èپAپ›‰ٌ‚إ•ش‚·ڈêچ‡‚ج1‰ٌ•ھ‚ج•شچد‹àٹz‚ً•ش‚µ‚ـ‚·پB
‚±‚ê‚ح‘S‚ؤ‚ج•شچد‹àٹz‚ھˆê’è‚إ‚ ‚錳—ک‹د“™•شچد‚إ‚جŒvژZژ®‚إ‚·پBپiپ¦Œ³—ک‚ئ‚حŒ³‹à+—ک‘§‚ًچ‡Œv‚µ‚½‚à‚ج‚إپA‚±‚ê‚ً‹د“™‚ةٹ„‚ء‚ؤ•شچد‚·‚é•û–@‚ًŒ³—ک‹د“™•شچد‚ئ‚¢‚¢‚ـ‚·پBپj
-
PMT (—ک—¦پ¦1
, ٹْٹشپ¦2
, Œ»چف‰؟’lپ¦3
, ڈ«—ˆ‰؟’lپ¦4
,ژx•¥ٹْ“ْپj
 |
—ل‡@پF
ڈZ‘îƒچپ[ƒ“‚جŒژپX‚ج•شچد‹àٹz‚ًŒvژZ‚·‚é
|
| پ@ |
A |
B |
|
1 |
ژط“ü‹à |
30,000,000‰~ |
|
2 |
‹à—کپi”Nپj |
2.475% |
|
3 |
•شچد‰ٌگ”پi”Nپj |
30”N |
ŒژپX‚ج•شچد‹àٹz‚ً‹پ‚ك‚ـ‚·پB‹à—ک‚ئ•شچد”Nگ”‚ج’Pˆت‚ھ”N‚ب‚ج‚إŒژ‚ة’¼‚µ‚ؤŒvژZ‚µ‚ـ‚·پB
-
PMT ( B2/12 ,
B3*12, B1 ,0
) پ¨
-118,147‰~
پ¦’چ
پ¦
ژہچغ‚ح118146.69پc
‚إ‚·‚ھExcel‚إ‚حژlژجŒـ“ü‚µ‚ؤ118147‚ھ•ش‚³‚ê‚ـ‚·پB
‚µ‚©‚µ‹âچs‚إ‚حگط‚èژج‚ؤŒvژZ‚ھٹî–{‚ب‚ج‚إپA‹âچs‚جƒVƒ~ƒ…ƒŒپ[ƒVƒ‡ƒ“ŒvژZ‚ب‚ا‚ةچ‡‚ي‚¹‚é‚ج‚إ‚ ‚ê‚خ118146‰~‚ئ‚¢‚¤‚±‚ئ‚ة‚ب‚è‚ـ‚·پBپiگ”ژ®‚ج’iٹK‚إگط‚èژج‚ؤ‚é‚ج‚إ‚ ‚ê‚خROUNDDOWNٹضگ”‚ً‘g‚فچ‡‚ي‚¹‚é•K—v‚ھ‚ ‚è‚ـ‚·پBچ،‰ٌ‚جڈêچ‡پAROUNDDOWN(PMT(B2/12,B3*12,B1,0),0)
‚ئ‚ب‚èپA118146‚ھ•ش‚³‚ê‚ـ‚·پBپj
پں ‚¨‚ـ‚¯پc‘چژx•¥ٹz‚حپH
118147پ~30پi”Nپjپ~12پپ42,532,811
‰~
‚¢‚©‚ة—ک‘§‚ھ‚ئ‚ç‚ê‚é‚©‚ھ•ھ‚©‚è‚ـ‚·‚ثپB
 |
—ل‡AپF
2%‚إ10000‰~‚ًژط‚èپA3‰ٌ‚إ•شچد‚·‚éڈêچ‡‚حپH
|
—ک—¦‚حپA•شچد1‰ٌ‚ ‚½‚è‚إژw’è‚·‚é•K—v‚ھ‚ ‚è‚ـ‚·پB‚و‚ء‚ؤ2%پ€3پپ0.67%‚ئ‚ب‚è‚ـ‚·پB
-
PMT ( 2%/3 ,
3 , 10000, 0
) پ¨
-3,378 ‰~
 |
—ل‡BپF
ƒ{پ[ƒiƒX•¥‚¢—L‚جƒچپ[ƒ“•شچد‚إپAŒژپX‚ج•شچدٹz‚ً‹پ‚ك‚é
|
ƒ{پ[ƒiƒX•¥‚¢—L‚جƒچپ[ƒ“•شچد‚àPMTٹضگ”‚إ•شچدٹz‚ً‹پ‚ك‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
ƒ{پ[ƒiƒX•¥‚¢‚جٹz‚حپAژط“ü‹à‚جپ“‚إژw’肵‚ؤ‚à‚¢‚¢‚إ‚·‚µپAٹz‚ًژw’肵‚ؤ‚à‚¢‚¢‚إ‚µ‚ه‚¤پB
پ@
پ¦
ڈًŒڈ
پiƒ{پ[ƒiƒX•¥‚¢‚ح”N2‰ٌ‚ئ‚·‚éپj
| پ@ |
A |
B |
|
1 |
ژط“ü‹à |
3000–œ |
|
2 |
‹à—کپi”Nپj |
2.475% |
|
3 |
•شچد‰ٌگ”پi”Nپj |
30”N |
|
4 |
ƒ{پ[ƒiƒX•ھ |
1000–œ |
پں
‚ـ‚¸‚حŒژپX‚ج•شچدٹz‚ً‹پ‚ك‚ـ‚·پB
-
PMT
پiB2/12
,
B3*12
,
B1-B4پ¦1
, 0 )
پ¨
-78,764
‰~
ژط“ü‹à‚©‚çƒ{پ[ƒiƒX•ھ‚ًˆّ‚¢‚½
ٹzپi2000–œپjپ¦1‚ًپA30پ~12‰ٌپA2.475پ“پ€12‚جŒژ—ک‚إ•شچد‚·‚éپA‚ئ‚¢‚¤ŒvژZ‚ة‚ب‚è‚ـ‚·پB
پں
ƒ{پ[ƒiƒX•¥‚¢1‰ٌ•ھ‚ج•شچدٹz‚ً‹پ‚ك‚ـ‚·پB
-
PMT
پiB2/2پ¦1
,
B3*2پ¦2
, B4
, 0 )
پ¨
-237,113
‰~
—ک—¦پ¦1
ژx•¥1‰ٌ•ھ‚ج—ک—¦‚ًڈo‚·•K—v‚ھ‚ ‚é‚ج‚إپA”N2‰ٌ•¥‚¢‚إ‚ ‚ê‚خ”N—کپ€2‚ئ‚µ‚ـ‚·پB
ٹْٹشپiژx•¥‰ٌگ”پjپ¦2
”N2‰ٌ‚ب‚ج‚إپA30”Nپ~2‚ئ‚µ‚ـ‚·پB
 |
—ل‡CپF
ŒژپXپ›‰~•شچد‚¾‚ئ‰½”N‚إ•ش‚¹‚éپH
|
PMTٹضگ”‚ح‹àٹz‚ئ—ک—¦پA•شچد”Nگ”‚ًژw’肵‚ؤپA–ˆŒژ‚ج•شچدٹz‚ًژژژZ‚إ‚«‚ـ‚·پB
‚إ‚ح‹t‚ة–ˆŒژ‚ج•شچدٹz‚ًژw’肵‚ؤ‰½”N‚إ•ش‚¹‚é‚©‚ًڈo‚·‚ة‚ح‚ا‚¤‚µ‚½‚ç‚¢‚¢‚إ‚µ‚ه‚¤پB
‚±‚ج‚و‚¤‚بڈêچ‡‚حپAƒSپ[ƒ‹ƒVپ[ƒN‚ًژg‚¢‚ـ‚·پB
پ@
پ¥
Œ»چف‚جڈًŒڈ
| پ@ |
A |
B |
|
1 |
ژط“ü‹à |
30000000‰~ |
|
2 |
‹à—کپi”Nپj |
2.475% |
|
3 |
•شچد‰ٌگ”پi”Nپj |
30”N |
|
4 |
ŒژپX‚ج•شچدٹz |
-118,147‰~ |
پ@
PMTٹضگ”‚ة‚و‚èپA30”N‚جڈêچ‡‚ح118147‰~‚ئ‚¢‚¤Œ‹‰ت‚ھڈo‚ؤ‚¢‚ـ‚·‚ھپAŒژپX15–œ‚ـ‚إ‚حڈo‚¹‚é‚ئ‚µ‚ـ‚·پBƒSپ[ƒ‹ƒVپ[ƒN‚إ‚حگ”ژ®‚جŒ‹‰تپi•شچدٹzپj‚ة‘خ‚µ–ع•W’lپiچ،‰ٌ‚ح150000پj‚ًگف’肵پAگ”ژ®‚إژg‚ء‚ؤ‚¢‚é
“ء’è‚جˆّگ”پiچ،‰ٌ‚ح•شچد‰ٌگ”پi”Nپjپj‚ً•د‰»‚³‚¹‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
-
گ”ژ®‚ھ“ü—ح‚³‚ê‚ؤ‚¢‚éƒZƒ‹پiB4پj‚ً‘I‘ً‚µپAپuƒcپ[ƒ‹پvپ|پuƒSپ[ƒ‹ƒVپ[ƒNپv‚ًƒNƒٹƒbƒN
پiEX2007‚جڈêچ‡‚حپuƒfپ[ƒ^پvƒ^ƒu-پuWhat-If•ھگح
پ¥پv-پuƒSپ[ƒ‹ƒVپ[ƒNپvپj
پ@
-
ˆب‰؛‚ج‚و‚¤‚ةژw’肵‚ـ‚·پB
پں
گ”ژ®“ü—حƒZƒ‹پپB4
پiPMTٹضگ”“ü—حƒZƒ‹پj
پں
–ع•W’l پپ
-150000پiگ”ژ®Œ‹‰ت‚ة‘خ‚µ–ع•W’l‚ًگف’èپj
پں
•د‰»‚³‚¹‚éƒZƒ‹پپB3پi•شچد”Nگ”پj
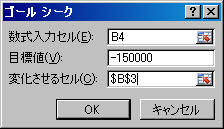
“ü—حŒمپAپuOKپv‚ًƒNƒٹƒbƒN
پ@
-
Œ‹‰ت‚ھ•\ژ¦‚³‚ê‚é‚ج‚إپA‚±‚ê‚إOK‚إ‚ ‚ê‚خپuOKپv‚ًƒNƒٹƒbƒN‚µپAŒ³‚ة–ك‚·‚ج‚إ‚ ‚ê‚خپuƒLƒƒƒ“ƒZƒ‹پv‚ًƒNƒٹƒbƒN
پ¨ “ڑپF21.5پi”Nپj
|